Delve into the intriguing world of mathematical expressions with “solve s 2 lw lh wh for w,” an equation that unveils its secrets through a journey of understanding, methods, and real-world applications. Embark on this intellectual adventure and discover the captivating insights that await you.

This expression, a symphony of variables and operators, beckons us to unravel its complexities. Join us as we dissect its components, explore the algebraic techniques for its solution, and uncover the practical scenarios where its mastery shines.

Understanding the Expression

The mathematical expression “solve s 2 lw lh wh for w” represents a problem where we aim to find the value of the variable ‘w’. To understand the expression, let’s break it down into its component parts:

Variables

• ‘s’ represents the surface area of a rectangular prism.
• ‘l’ represents the length of the prism.
• ‘w’ is the width of the prism, which we are trying to solve for.
• ‘h’ represents the height of the prism.

Operators

• ‘2’ is a numerical coefficient.
• ‘lw’ represents the multiplication of length and width.
• ‘lh’ represents the multiplication of length and height.
• ‘wh’ represents the multiplication of width and height.

Equation

The equation can be rewritten as:

s = 2(lw + lh + wh)

Methods for Solving: Solve S 2 Lw Lh Wh For W

Solving the expression 2s – 2lw – lh – wh for w requires algebraic manipulation. Here are two common methods to approach the problem:

Factoring

This method involves grouping terms with similar variables and factoring out common factors. Here’s how it works:

• Group the terms with w: 2lw + wh
• Factor out w from the grouped terms: w(2l + h)
• Rewrite the expression: 2s – w(2l + h) – lh
• Factor out -1 from the remaining terms: -1(2s + lh)
• Combine the factors: -1(2s + lh + w(2l + h))

Rearranging and Isolating

This method involves isolating the variable w on one side of the equation by performing algebraic operations:

• Add wh to both sides: 2s – 2lw – lh – wh + wh = 0
• Combine like terms: 2s – 2lw – lh = 0
• Subtract 2s from both sides: -2lw – lh = -2s
• Factor out -1 from the left-hand side: -1(2lw + lh) = -2s
• Divide both sides by -1(2l + h): w = (2s) / (2l + h)

Real-World Applications

Solving the expression s²lwlhwhhas practical applications in various fields, including architecture, engineering, and manufacturing.

For solving the equation s 2 lw lh wh for w, consider checking out the form 1120s schedule m 3 for more insights. This form provides detailed information on various aspects of tax calculations and can be a valuable resource for solving complex equations like s 2 lw lh wh for w.

In architecture, the expression can be used to calculate the surface area of a room or building, which is important for determining the amount of paint or wallpaper needed. In engineering, it can be used to calculate the volume of a container or the weight of a structure.

In manufacturing, it can be used to calculate the amount of material needed to produce a product.

Architecture

In architecture, the expression s²lwlhwhcan be used to calculate the surface area of a room or building. The surface area is the total area of all the surfaces of the room or building, including the walls, ceiling, and floor. To calculate the surface area, the length ( l), width ( w), and height ( h) of the room or building must be known.

For example, if a room is 10 feet long, 8 feet wide, and 9 feet high, the surface area would be:

s²lwlhwh= 2(10 ft x 8 ft) + 2(10 ft x 9 ft) + 2(8 ft x 9 ft) = 346 sq ft

Related Concepts

Understanding the expression s = 2lw + 2lh + 2wh requires familiarity with several related mathematical concepts:

Surface Area

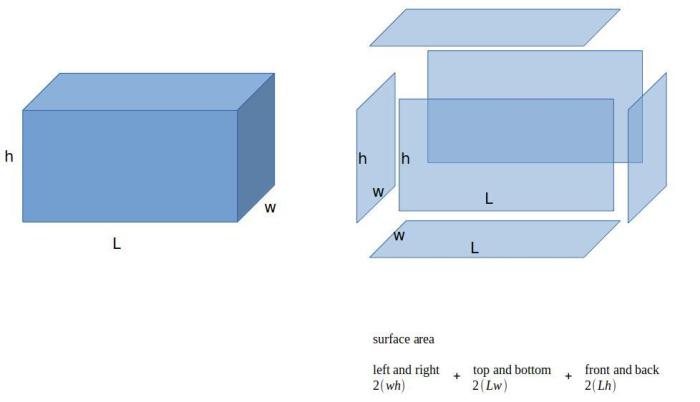
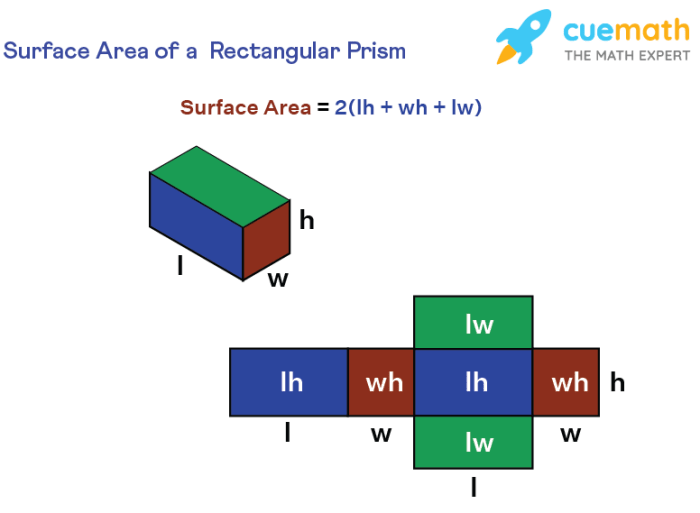
Surface area refers to the total area of a surface. In the case of a rectangular prism, the surface area is the sum of the areas of its six faces. The formula for surface area is:

S = 2lw + 2lh + 2wh

where: – S represents the surface area – l represents the length of the prism – w represents the width of the prism – h represents the height of the prism

Perimeter

Perimeter is the distance around the boundary of a shape. In the case of a rectangle, the perimeter is the sum of the lengths of its four sides. The formula for the perimeter of a rectangle is:

P = 2(l + w)

where:

• P represents the perimeter
• l represents the length of the rectangle
• w represents the width of the rectangle

Volume

Volume is the amount of space occupied by a three-dimensional object. In the case of a rectangular prism, the volume is calculated by multiplying its length, width, and height. The formula for the volume of a rectangular prism is:

V = lwh

where:

• V represents the volume
• l represents the length of the prism
• w represents the width of the prism
• h represents the height of the prism

These related concepts provide a framework for understanding and solving the expression s = 2lw + 2lh + 2wh, which represents the surface area of a rectangular prism.

Extensions and Variations

The expression s = 2lw + 2lh + 2wh provides a basic formula for calculating the surface area of a rectangular prism. However, there are variations of this expression that introduce additional complexity.

Modified Dimensions

One variation involves modifying the dimensions of the prism. For example, if the prism is a cube, all three dimensions (length, width, and height) are equal. In this case, the surface area formula becomes s = 6s^2, where s represents the side length of the cube.

Additional Surfaces

Another variation considers additional surfaces on the prism. For instance, if the prism has a triangular or circular base, the surface area formula needs to be adjusted to account for the additional surface area.

Variations in Shape, Solve s 2 lw lh wh for w

The expression can also be modified to calculate the surface area of other shapes, such as cylinders, cones, or spheres. These variations involve different formulas that take into account the unique geometric properties of each shape.

General Inquiries

What is the purpose of solving “solve s 2 lw lh wh for w”?

Solving this expression allows us to isolate the variable “w” and determine its value based on the given values of “s,” “l,” “w,” “h,” and “wh.”

What are the different methods for solving this expression?

There are several methods, including substitution, elimination, and using the properties of equality.

Can you provide an example of a real-world application of this expression?

This expression finds use in calculating the volume of a rectangular prism, where “s” represents the surface area, “l” the length, “w” the width, “h” the height, and “wh” the product of width and height.