Embark on a comprehensive exploration of geometry chapter 5 review answers, where the fundamental principles of geometry unfold, providing a solid foundation for understanding the intricacies of shapes, angles, and their real-world applications.
Delving into the heart of geometry, this review encompasses key concepts, theorems, and properties, empowering learners to grasp the essence of this fascinating subject and its practical significance in various fields.
Geometry Chapter 5 Review: Basic Concepts: Geometry Chapter 5 Review Answers

Geometry Chapter 5 introduces the fundamental concepts of points, lines, planes, and angles. These building blocks of geometry are essential for understanding more complex geometric figures and their relationships.
Points represent locations in space, lines extend infinitely in one direction, and planes are flat surfaces that extend infinitely in two dimensions. Angles are formed by the intersection of two rays or line segments and are measured in degrees.
These basic concepts have numerous applications in the real world. For instance, points can be used to represent the locations of cities on a map, lines can be used to model roads or boundaries, and planes can be used to represent surfaces like floors or walls.
Angle Relationships and Theorems
Chapter 5 also explores different types of angle relationships, including complementary, supplementary, and vertical angles. Complementary angles add up to 90 degrees, supplementary angles add up to 180 degrees, and vertical angles are opposite angles formed by intersecting lines.
The Angle Bisector Theorem states that the angle bisector of a triangle divides the opposite side into segments proportional to the lengths of the adjacent sides. This theorem has applications in various fields, such as architecture and engineering.
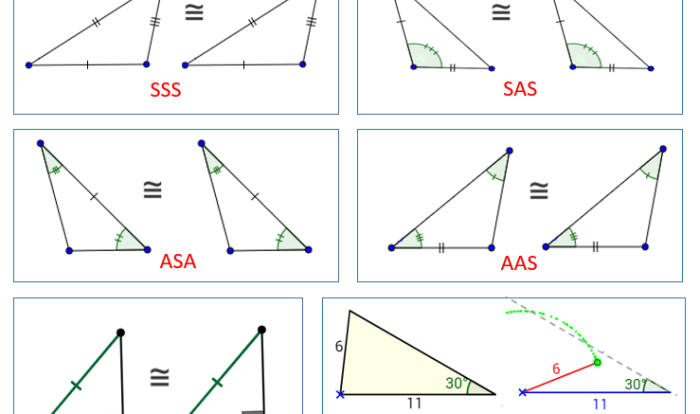
Triangle Congruence and Similarity
Chapter 5 discusses the criteria for triangle congruence and similarity. Two triangles are congruent if they have the same shape and size, while two triangles are similar if they have the same shape but not necessarily the same size.
The Side-Side-Side (SSS), Side-Angle-Side (SAS), and Angle-Side-Angle (ASA) criteria can be used to prove triangles congruent. The Angle-Angle-Side (AAS) and Side-Side-Angle (SSA) criteria can be used to prove triangles similar.
Special Quadrilaterals
Special quadrilaterals, such as parallelograms, rectangles, squares, and trapezoids, are also covered in Chapter 5. These quadrilaterals have specific properties that distinguish them from other quadrilaterals.
Parallelograms have opposite sides parallel, rectangles have four right angles, squares are rectangles with equal sides, and trapezoids have one pair of parallel sides.
Circles and Their Properties
Chapter 5 introduces the basic properties of circles, including radius, diameter, and circumference. The radius is the distance from the center of the circle to any point on the circle, the diameter is the distance across the circle through the center, and the circumference is the distance around the circle.
Different types of circles, such as tangent circles and intersecting circles, are also discussed. Tangent circles touch at one point, while intersecting circles cross at two points.
Applications of Geometry in Real-World Problems, Geometry chapter 5 review answers
Geometry is not just a theoretical subject; it has numerous applications in the real world. For example, geometry is used in architecture to design buildings, in engineering to design bridges and machines, and in design to create visually appealing products.
Understanding geometry is essential for solving real-world problems that involve spatial relationships and measurements. It helps us to make informed decisions and design effective solutions.
FAQ Guide
What are the key concepts covered in geometry chapter 5?
Geometry chapter 5 delves into fundamental concepts such as points, lines, planes, and angles, providing a solid foundation for understanding the subject.
How are angle relationships classified?
Angle relationships are categorized into complementary, supplementary, and vertical angles, each with distinct properties and applications.
What criteria determine triangle congruence and similarity?
Triangles can be proven congruent or similar based on specific criteria, including side-side-side (SSS), side-angle-side (SAS), angle-side-angle (ASA), and angle-angle-side (AAS) congruency, as well as angle-angle (AA) and side-side-side (SSS) similarity.
What are the different types of special quadrilaterals?
Special quadrilaterals include parallelograms, rectangles, squares, and trapezoids, each with unique properties and theorems associated with them.
How is geometry applied in real-world problems?
Geometry finds practical applications in architecture, engineering, design, and various other fields, enabling us to understand and solve complex problems involving shapes, angles, and measurements.