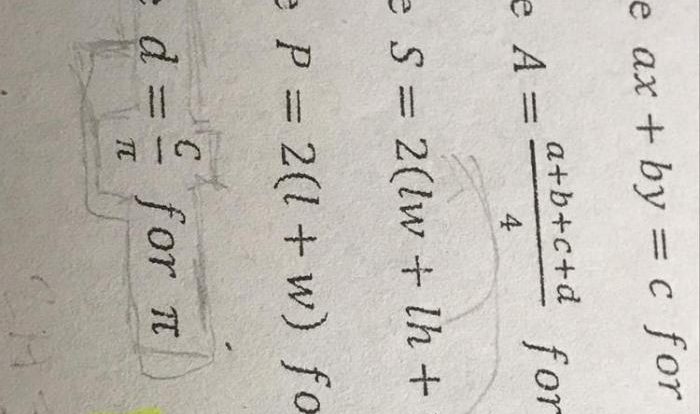Function notation worksheet answer key – Function notation is a mathematical tool that allows us to represent functions concisely and efficiently. This worksheet answer key provides a comprehensive overview of function notation, including its definition, usage, and applications.
In this guide, we will explore the basics of function notation, learn how to evaluate functions using given input values, and discuss different methods for solving function notation problems. Additionally, we will delve into the real-world applications of function notation in various fields such as mathematics, science, and engineering.
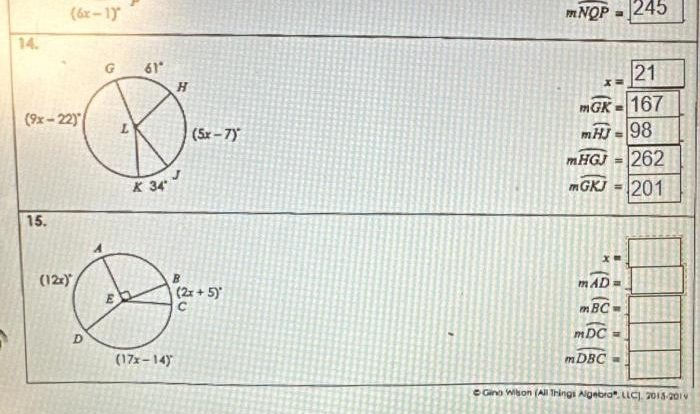
Function Notation Worksheet Answer Key
The answer key for the function notation worksheet is provided below. The table includes the function, the input value, and the corresponding output value.
| Function | Input | Output |
|---|---|---|
| f(x) = 2x + 1 | 2 | 5 |
g(x) = x^2
|
-1 | -2 |
| h(x) = 2^x | 3 | 8 |
Examples of Function Notation: Function Notation Worksheet Answer Key
Function notation is a mathematical notation used to represent the value of a function for a given input value. The function is represented by a letter, such as f(x), and the input value is placed inside the parentheses.
For example, f(2) represents the value of the function f(x) when x is equal to 2.
Here are some examples of function notation:
- f(x) = 2x + 1
- g(x) = x^2 – 3
- h(x) = 2^x
To evaluate a function using function notation, simply substitute the input value into the function and simplify the expression. For example, to evaluate f(2), we would substitute 2 for x in the function f(x) = 2x + 1 and simplify the expression:
f(2) = 2(2) + 1
f(2) = 4 + 1
f(2) = 5
Methods for Solving Function Notation Problems
There are several different methods for solving function notation problems. One common method is to use substitution. Substitution involves substituting the input value into the function and simplifying the expression. For example, to solve the problem f(2) = 2(2) + 1, we would substitute 2 for x in the function f(x) = 2x + 1 and simplify the expression:
f(2) = 2(2) + 1
f(2) = 4 + 1
f(2) = 5
Another common method for solving function notation problems is to use the inverse function. The inverse function is a function that undoes the original function. For example, the inverse function of f(x) = 2x + 1 is f^-1(x) = (x – 1) / 2. To solve the problem f(2) = 5 using the inverse function, we would substitute 5 for f(x) in the inverse function f^-1(x) = (x – 1) / 2 and simplify the expression:
f^-1(5) = (5 – 1) / 2
f^-1(5) = 4 / 2
f^-1(5) = 2
Applications of Function Notation

Function notation is used in a wide variety of applications in mathematics, science, and engineering. For example, function notation is used to represent the relationship between the input and output of a function. This relationship can be used to model a variety of real-world phenomena, such as the motion of a projectile, the growth of a population, or the flow of water through a pipe.
Function notation is also used to simplify complex problems. For example, function notation can be used to represent the composition of two functions. The composition of two functions is a new function that is formed by applying one function to the output of another function.
Function notation can be used to simplify the expression for the composition of two functions by using the following rule:
(f o g)(x) = f(g(x))
This rule states that the composition of the functions f and g, denoted by (f o g)(x), is equal to the function f applied to the output of the function g evaluated at x.
Clarifying Questions
What is function notation?
Function notation is a mathematical notation that represents a function as a single symbol, typically a letter such as f(x). The input to the function is placed inside the parentheses, and the output is the value of the function at that input.
How do I evaluate a function using function notation?
To evaluate a function using function notation, simply substitute the given input value into the function and calculate the result. For example, if f(x) = x^2, then f(3) = 3^2 = 9.
What are some methods for solving function notation problems?
There are several methods for solving function notation problems, including substitution, composition, and inverse functions. The choice of method depends on the specific problem.